Back in November, I finished my little niece Zoe’s Prime Factorization Blanket!
What is a Prime Factorization Blanket? Why, a blanket that shows the prime factorization of all the whole numbers up to 99, using a color for each prime number.
This is the same set-up as my niece Arianna’s Prime Factorization Blanket, as a matter of fact. But I used new colors for Zoe’s blanket, going with a lot of pink, because we already knew she was going to be a girl. (With Arianna, we found out she’d be a girl right when I got to the number 17, so in that blanket 17 is pink.)
The blankets don’t really need a pattern, but here are the specifications: I used Tahki Cotton Classic yarn, because it has so many shades available. Each square is a garter stitch square with 12 ridges and 12 stitches, which is easy to divide in 2, 3, 4, or 6 sections. For 5 sections, I did a plain row at the beginning and end. It’s done in entrelac, so you go across and knit the square for each number individually, then go back making the white squares, then do the next row of numbers, then a row of white. It’s much nicer than making the original sweater, because you can work on one number at a time, and don’t have to carry yarn across.
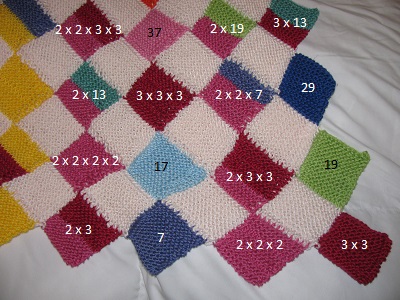
Here is Zoe’s Prime Factorization Blanket laid out flat (or sort of flat):
Here’s how it works. Starting in the bottom left corner (because graphs always have the origin in the bottom left), there’s a missing space for zero. Then 1 is pale pink, the background color:
2 was assigned the color pink.
3 was assigned the color red.
4 is our first composite number, 2 x 2. So I used two sections of pink. (If you look at the actual blanket, you can tell there are two sections, but it’s harder to tell in the picture.)
5 is prime, so it’s assigned a new color, yellow.
6 is composite, 2 x 3. So it gets a section of pink and a section of red.
7 is prime, so it gets a new color, purple.
8 is composite, 2 x 2 x 2. Three sections of pink.
9 = 3 x 3, so it gets two sections of red.
New row, so look back at the photo of the bottom right.
10 = 2 x 5, so it gets a section of pink and a section of yellow.
11 is prime, so it gets a new color, turquoise.
12 = 2 x 2 x 3, so two sections of pink and one section of red.
13 is prime, so it gets a new color, sea foam green.
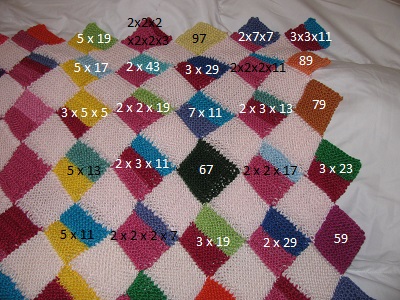
Now the picture for the middle:
14 = 2 x 7, so pink and purple.
15 = 3 x 5, so red and yellow.
16 = 2 x 2 x 2 x 2, so four sections of pink.
Now the picture of the right side:
17 is prime, so it gets a new color, baby blue.
18 = 2 x 3 x 3, one section of pink, two sections of red.
19 is prime, so it gets a new color, olive green.
The next row starts at 20. The blanket goes all the way up to 99.
Here’s the top corner, so you can see some bigger numbers:
You can see the patterns nicely in the grid of the blankets. As an example of some simple patterns, the twos and fives line up in straight lines, but so do the elevens, in a diagonal line. There are lots more patterns which you can find the more you look at the blanket.
And Zoe likes it!
I’m gathering all my Mathematical Knitting links on my Sonderknitting page. (I hope to soon add coloring pages, too!) Check out the rest!