I’ve posted several Prime Factorization Coloring Sheets on my Sonderknitting page lately.
I decided I should try coloring them myself, so I could post a thumbnail of each one. I had a lot of fun doing it, and was reminded of lots of cool properties I discovered from knitting my prime factorization sweater and looking at these charts.
I have a manuscript for a math-related children’s nonfiction book about using math to make codes with colors. Originally, I put several of these charts into the book — but I eventually decided it was a distraction and decided to put them on my website instead.
But they show all sorts of cool things!
First, there’s the ten-by-ten prime factorization chart using ordinary, decimal numbers.
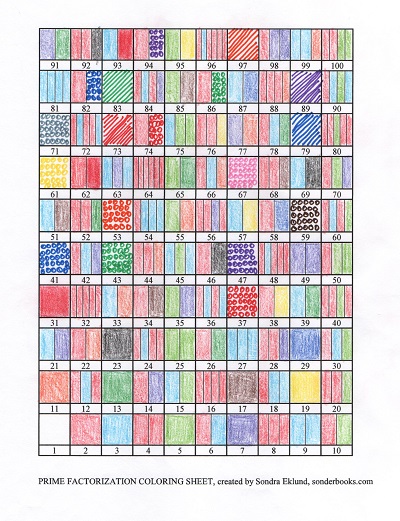
Coloring this chart gives you a great feeling for factorization and multiples. I posted about watching a second grader color it. I think of it as more for older kids, who are learning about primes and multiples, or indeed adults, in keeping with the adult coloring book craze. But watching a second grader color it assured me that it can give insights to anyone. (I made the instructions such that you don’t even have to know how to multiply. Just color every second square the color for 2, every third square the color for 3, and so on.)
Now, in my original sweater, I put rows of 8 on the back and rows of 2 and rows of 3 on the sleeves. The prime factorization charts in different bases are the same idea.
First, they give you a feeling for how different bases work.
Here’s the sheet for octal, base 8:
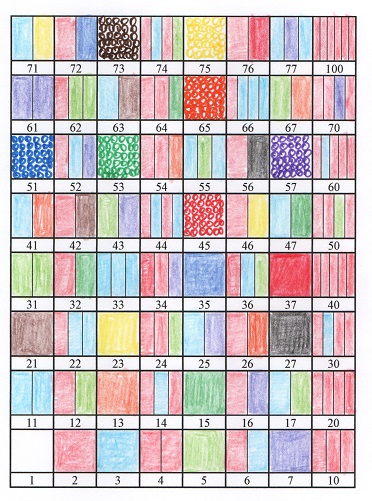
You can color it exactly the same way as you did the ten-by-ten chart. Color every second square with the color for 2, every third with the color for 3, and so on. If you take the time to do that, you’ll grasp how the numbers count up to 7 and then use the next digit, since place value in octal gives the ones digit, the eights digit, and the sixty-fours digit.
The chart also makes a good way to translate between octal and decimal. (Though you can just multiply the eights digit times eight and add the ones digit.)
But I enjoy some of the other patterns.
The first, most obvious pattern is that in the decimal chart, the multiples of 5 and the multiples of 2 line up vertically (as well as the multiples of 10, which are both). That’s because 10 = 2 x 5.
In the octal chart, the multiples of 2 line up vertically, since 8 = 2 x 2 x 2. So do the multiples of 4 — each with two factors of 2, and the multiples of 8 — each with three factors of 2.
In the Base 6 chart, as you’d expect, the multiples of 2 and the multiples of 3 line up vertically. (And the multiples of 6, with a factor of 2 and a factor of 3, do as well.)

But it’s also fun what happens to the color for Base Plus One and Base Minus One.
In the 10×10 chart, look at what happens to the color for 11, orange, and the multiples of 11. They go diagonally to the right up the chart: 11, 22, 33, 44, . . .
In the 10×10 chart, 9 is represented by two sections of blue, for 3 x 3. These colors go diagonally up the chart in the opposite direction: 9, 18, 27, 36, . . .
In the 8×8 chart, the octal number 11 is the decimal number 9 — so it is still represented by two sections of blue. But since 9 is one bigger than our base in that chart, the two sections of blue go diagonally up the chart to the right — just like 11 in the decimal chart.
In the octal chart, the color for 7, purple, goes diagonally up the chart to the left, with the octal numbers 7, 16, 25, 34, . . . .
In the 6×6 chart, we’ve got the same patterns, this time with 7 (which is 11 in base six) and 5.
7 (purple) goes diagonally right up the chart, and 5 goes diagonally left up the chart.
And we’ve got the same patterns in a 7×7 Base Seven chart:

Notice that since 7 is prime, no colors line up except purple, the color for 7.
And the colors for 8 and 6 go diagonally up the chart.
The Hexadecimal chart in base 16 is even more interesting:

Notice how all the multiples of 2 line up vertically, with multiples of 4, 8, and 16 also lined up.
11 in Base 16 is decimal 17, which is brown, and it acts like all the other 11s, going diagonally up and to the right.
1 less than 16 is F = 15, and the blue and green colors for F go diagonally up and to the left.
Before I finish I want to mention one more pattern I noticed from looking at these charts. It’s the familiar trick in Base 10 of the rule for figuring out if any number is a multiple of 9: Just add up the digits, and they will be a multiple of 9.
The reason this works is that 10 is congruent to 1 mod 9.
In base 10, each decimal place represents a number multiplied by a power of 10.
In base 9, that’s going to be the same as multiplying by 1 — so if you add up the digits, you get what the number is congruent to mod 9.
If none of that made any sense to you, just know this:
If you add up the digits of a base 10 number (and if you get a number bigger than 9, add them up again), your result is the remainder you’ll get if you divide the number by 9.
Since multiples of 9 have no remainder when divided by 9 — the digits of multiples of 9 in base 10 always add up to multiples of 9. (And by the same reasoning, the digits of multiples of 3 in base 10 always add up to multiples of 3.)
But you might have noticed when looking at the diagonal colors:
In Base 8, the digits of multiples of 7 always add up to multiples of 7.
In Base 6, the digits of multiples of 5 always add up to multiples of 5.
In Base 7, the digits of multiples of 6 always add up to multiples of 6.
And the digits of multiples of 2 always add up to multiples of 2.
And the digits of multiples of 3 always add up to multiples of 3.
(Use the colors to tell which numbers these are in Base 7.)
In Base 16, the digits of multiples of F (15) always add up to multiples of F.
And the digits of multiples of 5 always add up to multiples of 5.
And the digits of multiples of 3 always add up to multiples of 3.
(Use the colors to tell which numbers these are in Base 16.)
Forgive me, but I think these patterns are Awesome!
Let’s face it, you’ll see them much more clearly if you color the charts yourself!
Download the coloring charts at Sonderknitting!
Happy Coloring!



























