Prime Factorization – Page 2

Jan 16, 2016January 16, 2016

Zoe’s Prime Factorization Blanket!

Back in November, I finished my little niece Zoe’s Prime Factorization Blanket!

What is a Prime Factorization Blanket? Why, a blanket that shows the prime factorization of all the whole numbers up to 99, using a color for each prime number.

This is the same set-up as my niece Arianna’s Prime Factorization Blanket, as a matter of fact. But I used new colors for Zoe’s blanket, going with a lot of pink, because we already knew she was going to be a girl. (With Arianna, we found out she’d be a girl right when I got to the number 17, so in that blanket 17 is pink.)

The blankets don’t really need a pattern, but here are the specifications: I used Tahki Cotton Classic yarn, because it has so many shades available. Each square is a garter stitch square with 12 ridges and 12 stitches, which is easy to divide in 2, 3, 4, or 6 sections. For 5 sections, I did a plain row at the beginning and end. It’s done in entrelac, so you go across and knit the square for each number individually, then go back making the white squares, then do the next row of numbers, then a row of white. It’s much nicer than making the original sweater, because you can work on one number at a time, and don’t have to carry yarn across.

Here is Zoe’s Prime Factorization Blanket laid out flat (or sort of flat):

Here’s how it works. Starting in the bottom left corner (because graphs always have the origin in the bottom left), there’s a missing space for zero. Then 1 is pale pink, the background color:

2 was assigned the color pink.
3 was assigned the color red.

4 is our first composite number, 2 x 2. So I used two sections of pink. (If you look at the actual blanket, you can tell there are two sections, but it’s harder to tell in the picture.)
5 is prime, so it’s assigned a new color, yellow.
6 is composite, 2 x 3. So it gets a section of pink and a section of red.

7 is prime, so it gets a new color, purple.
8 is composite, 2 x 2 x 2. Three sections of pink.
9 = 3 x 3, so it gets two sections of red.

New row, so look back at the photo of the bottom right.
10 = 2 x 5, so it gets a section of pink and a section of yellow.
11 is prime, so it gets a new color, turquoise.
12 = 2 x 2 x 3, so two sections of pink and one section of red.
13 is prime, so it gets a new color, sea foam green.

Now the picture for the middle:
14 = 2 x 7, so pink and purple.
15 = 3 x 5, so red and yellow.
16 = 2 x 2 x 2 x 2, so four sections of pink.

Now the picture of the right side:
17 is prime, so it gets a new color, baby blue.
18 = 2 x 3 x 3, one section of pink, two sections of red.
19 is prime, so it gets a new color, olive green.

The next row starts at 20. The blanket goes all the way up to 99.

Here’s the top corner, so you can see some bigger numbers:

You can see the patterns nicely in the grid of the blankets. As an example of some simple patterns, the twos and fives line up in straight lines, but so do the elevens, in a diagonal line. There are lots more patterns which you can find the more you look at the blanket.

And Zoe likes it!

I’m gathering all my Mathematical Knitting links on my Sonderknitting page. (I hope to soon add coloring pages, too!) Check out the rest!

Oct 14, 2015October 14, 2015

My Prime Factorization Hairnet

Mathematical, Prime Factorization 0

Our church is having a Stop Hunger Now Food Packaging Event next Sunday, October 18, 2015. As a form of publicity for the event, they’ve asked us to decorate a hairnet and take a selfie.

That was the moment I realized: I have a Prime Factorization Sweater, a Prime Factorization Cardigan, a Prime Factorization Scarf, a Prime Factorization T-Shirt, and have made Prime Factorization Blankets. But I didn’t have a Prime Factorization Hairnet!

Well, I soon remedied that!

Okay, it’s not knitting. But I printed a chart I’d made of numbers color-coded with their prime factorization for the Prime Factorization T-shirt. Then I simply cut out the individual squares and glued them to the hairnet in a spiral pattern. So it goes from 1 to 100.

How it works? Each prime number gets a new color. Composite numbers are divided into sections with a section for each factor. Each section is colored according to that prime’s color. For example, 42 = 2 x 3 x 7, so the square for 42 is divided into three sections, colored blue for 2, red for 3, and green for 7.

This selfie not only shows the Prime Factorization Hairnet, it also gives a glimpse of infinity!

Oh, and I’m gathering all my Mathematical Knitting (and other mathematical creations) at Sonderknitting. Eventually, I’ll add mathematical explanations and patterns and activities and other good things.

I can safely say that mine is the most educational hairnet selfie posted yet!

May 19, 2015February 8, 2016

Pascal’s Triangle Shawl #2

Mathematical, Prime Factorization 3

Hooray! Hooray! Today I finished my second, prettier Pascal’s Triangle Shawl!

Pascal’s Triangle is the triangle with 1s on the edges, where each entry is the sum of the two entries above it.

So the beginning rows work like this:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1

Now, what I did was choose a color of yarn for each prime. Then each entry in the triangle is factored, and each number is shown by the colors of its factors.

I did the same thing with my first Pascal’s Triangle Shawl. With this one, since there are only the primes 2, 3, 5, 7, 11, and 13, I decided to use progressively darker shades of pink and purple, so the shawl would gradually get darker.

Here is a closer look at a section of the shawl:

This next picture shows that along the second row, we have the numbers simply in sequence.

For math nuts, each row also contains the binomial coefficients, the coefficients in the expansion of
(a+b)^n

This means that the rth entry in the nth row can be calculated with the formula:
n!/(n-r)! (Counting the entries in each row as 0 through n.)

Some examples: The 2nd entry in the 5th row is (5×4)/(2×1) = 10

The 3rd entry in the 7th row is (7x6x5)/(3x2x1) = 35

Now, I factor all the numbers in my shawl, so for big numbers, it doesn’t matter what the actual number is, but the factorization is easy from the formula.

For example, the 4th entry in the 15th row is (15x14x13x12)/(4x3x2x1) = 3x5x7x13

You can see some of the bigger numbers in this picture:

Now, there are a couple of characteristics which I believe make the shawl especially beautiful.

One is that because these are the binomial coefficients, once you get to the row of a prime number, every entry in that row has the prime for a factor.

This is easier to see with the actual shawl in front of you, but here again is the big picture. You can see that once a new color starts, it goes all the way across the row.

What’s more, by the distributive law, since every entry in a prime row has that prime as a factor, all the sums of those numbers will also have the prime for a factor — and we end up having inverse triangles of each color.

Here’s some more detail:

Of course, the very coolest thing about it is that, even if you have no idea of the math involved, the combination is beautiful.

And that simply makes me happy.

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Nov 3, 2014February 27, 2016

Oops! Can you find the mistake?

Mathematical, Prime Factorization 2

Oops! Today I realized I had used the wrong shade in one of the rows of my prime factorization cardigan. I remembered I had discovered that in the process of knitting, and had planned to go over the offending line with duplicate stitch. But I forgot — so now I think I will use it as a puzzle. Can you spot the number that is out of place?

You’ll definitely need a closer look at the cardigan.

Who will be the first person to spot the error? (You can use the comments to inform me.) This person is almost as geeky as me! 🙂 Though at least I can restrain myself from taking apart the cardigan. There was an error in my Prime Factorization Sweater — but it was one of five factors of a number (probably 72), so it only involved four stitches in the wrong color. I was able to pick them out, then reinsert the right color with a yarn needle.

Oh, I should say that the error is not in row 48, which is 2 x 2 x 2 x 2 x 3. I didn’t want to have the pink thread loose over all four blue stitches, so I twisted the yarn after two stitches — and it ended up showing up a bit on the front, though not as much as an actual wrong stitch.

No, the error is a matter of using the wrong shade in one of the stripes. The result would be far too large a number for this sweater. And now I can use it to find out who is paying attention. 🙂

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Nov 3, 2014February 8, 2016

My Prime Factorization Cardigan

Mathematical, Prime Factorization 27

I did it! More than two years after beginning, I have finally completed my Prime Factorization Cardigan!

Here’s how it works! The stripes each represent a counting number. They go from left to right, cuff to cuff. 1 is black, the background color (which is a factor of everything). Then each prime gets a new color. 2 is blue; 3 is pink; 5 is yellow; 7 is purple….

Composite numbers get the combination of colors for their factors. 6 = 2 x 3, so it’s alternating blue and pink. 10 = 2 x 5, so blue and yellow. 12 = 2 x 2 x 3, so two stitches of blue followed by one of pink….

Perfect powers get multiple rows. 4 = 2 x 2, so two rows of blue; 8 = 2 x 2 x 2, so three rows of blue; 9 = 3 x 3, so two rows of pink. I think my favorite is 36 = 2 x 2 x 3 x 3, so I did two rows of alternating blue and pink.

I put labels in one picture, to give the pattern:

As for details, I used Plymouth Encore yarn, 75% acrylic, 25% wool — it is not expensive and comes in many colors. I looked online for a pattern knitted cuff-to-cuff, and found this Rainbow Lace Jacket. I of course changed the colors. I knitted the stripes in garter stitch, and the rows in between the stripes in black stockinette.

And now for more pictures! First, an overall look at the sweater again:

And with the arms down:

And the back: (I decided to make the numbers go two-dimensionally across the sweater, from cuff to cuff. So the back is a mirror of the front.)

And here’s more detail, Numbers 17 to 32 (The powers of 2 are easy to spot! They are the multiple rows of blue.):

Then Numbers 26 to 38:

34 to 47:

41 to 58:

51 to 63:

And finally, 64 to 78:

There you have it! The latest in my prime factorization knitting adventures. Let’s see, I feel compelled to summarize what I’ve done.

It began with the Prime Factorization Sweater.

Then when that became wildly popular on the internet, I made a Prime Factorization T-shirt. (These are available for sale, by the way.)

I experimented with stripes when I made my Prime Factorization Scarf, and planned out how to do this cardigan.

Then my siblings were expecting babies. For my sister’s baby, I knitted a Coded Blessing Blanket.

For my brother’s baby, nothing but a Prime Factorization Blanket would do.

Which got me going on a Pascal’s Triangle Shawl.

Which got me to start another, prettier one (Still not finished).

And brings me back to the Prime Factorization Cardigan!

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Feb 13, 2014February 8, 2016

My Pascal’s Triangle Shawl

Mathematical, Prime Factorization 3

I finished my Pascal’s Triangle Shawl!

I’m very happy with how it turned out!

In fact, I was disappointed by how the top edge curled — until I wore it, and it forms into a sort of collar! Perfect!

I already explained the math behind the shawl in great detail.

So now I’ll just say that this is a color-coded representation of Pascal’s Triangle, with a color for each prime factor, and each number represented in a diamond with its prime factorization shown.

In Pascal’s Triangle (at least when it’s shown with the point down, as above), each number is the sum of the two numbers beneath it, with 1 on all the ends. So 1 is white in my shawl.

The color scheme I used for the rest was:

2 is turquoise.
3 is yellow.
5 is red.
7 is purple.
11 is pink.
13 is light blue.

I took it up to the 15th row. After that, entries had more than 6 factors, so it wouldn’t be as easy to get them all in.

Take a moment to enjoy the flow. 🙂 Each time we get to a prime, every number in that row has that prime as a factor.

And the next row has that prime factor in all but the ends, and so it continues, forming an inverse triangle of that color. (This is because of the distributive law, as I explained in my earlier post.)

Looking at this shawl simply makes me happy. And I’m tremendously proud of it. I think it’s safe to say that this is the first Pascal’s Triangle Shawl ever knitted. 🙂

But it won’t be the last! As I began the shawl, I wasn’t sure it wasn’t a bit too garish with all the bright colors right next to each other. At least in the prime factorization blanket, I had rows of white in between the numbers. Though now that it’s finished, I completely love it.

Anyway, I decided to make a second one — this time using shades of pink and purple, with only subtle differences, going from light to dark. The first one will be easier to use for explaining the math, but I think the second one may be prettier.

And last night, I got another idea about how to make the second one different. Instead of having blocks of color for each factor, I’m planning to alternate rows. I think that will blend the colors as you look at the shawl — and I think it will be very beautiful! Stay tuned!

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Nov 28, 2013February 8, 2016

Pascal’s Triangle Shawl to Row 10

Mathematical, Prime Factorization 1

Hooray! I’ve knitted my Pascal’s Triangle Shawl all the way to the 10th row!

Now, it’s not finished — I’m going up to 15 — but I can’t resist explaining it already. I think it is SO COOL! And even more patterns are going to pop out as I continue.

My mathematical knitting began with my Prime Factorization Sweater, done in intarsia, with Tahki’s Cotton Classic yarn. It shows the prime factorization of all the numbers from 2 to 100, using a different color for each prime, with 1, the background color, in white.

Later when the internet discovered my sweater, I made a Café Press Prime Factorization T-shirt so anyone can have the color-coded prime factorization of the numbers from 2 to 100.

Now, the trouble with intarsia, is you have to carry all the colors you use in any given row along the back of the sweater. And there are about a million ends to sew in at the end. But a couple years ago, I got a hankering to do something like this again, and it occurred to me that if I used stripes, I could deal with one color at a time. I made a reversible Prime Factorization Scarf, where the thickness of the stripes tells you how many times a factor occurs. It also uses a different color for each prime. This time 1 is black, and there is a black stripe between each successive number. Within each number, there is a two-row stripe for each factor. This is done in Plymouth Encore yarn.

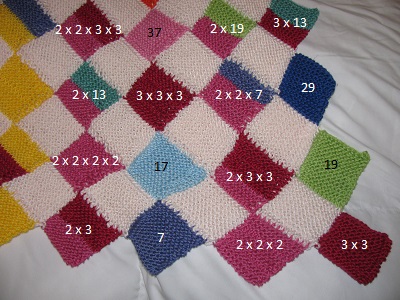
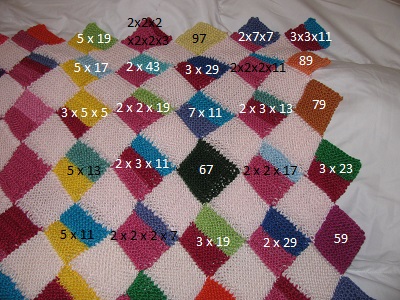
Then my brother, even more mathematically minded than me (if you can believe that!) was going to become a father. His daughter needed a prime factorization blanket! And it occurred to me that it would be far easier to knit the design in Intrelac, using rows of diamonds. I went back to the nice soft Cotton Classic yarn, and white as 1, to be bright for the baby. I used garter rows to show how many factors of each color.

The Prime Factorization Blanket turned out fantastic! But the horrible part was giving it away.

I got to thinking. Intrelac naturally falls into a triangle shape. I instantly thought of something mathematical in the shape of a triangle — Pascal’s Triangle! And I have a special fondness for Pascal’s Triangle, having won a Chalk Talk competition on the Binomial Theorem at a Math Field Day when I was a junior in high school. The numbers in Pascal’s Triangle are the Binomial Coefficients from the Binomial Theorem.

And — here’s where I started getting excited — I knew that there are some fascinating patterns in Pascal’s Triangle. Why not show the prime factorization of each number in the triangle? That would show some of the patterns.

So I began my Pascal’s Triangle Shawl. The first thing I noticed when sketching it out is very cool. Even though the numbers in the middle of the triangle get hugely big quite quickly, they never have any prime factors bigger than the number on the end of the row. So if I take the shawl to row 15, I will only need colors for 1, 2, 3, 5, 7, 11, and 13. To show the prime factorization this way (the same as the blanket), I’ll use 12 x 12 squares, using garter stitch rows to show the factors, with smooth stockinette stitch between factors.

The numbers in Pascal’s Triangle can be calculated two ways. The first way, each number is just the sum of the two numbers above it. Starting with 1.

So the 0th row is 1.

The 1st row is 1 1.

The 2nd row is 1 2 1. We get the 2 by adding the 1 and 1 above it.

The 3rd row is 1 3 3 1.

The 4th row is 1 4 6 4 1.

The 5th row is 1 5 10 10 5 1

The 6th row is 1 6 15 20 15 6 1.

And so on. In the blanket, you can figure out what number each color represents by looking on the edges.

Here it is again:

You can see that I’ve used white for 1. 2 is blue. 3 is yellow. 5 is red. 7 is purple.

You can’t see the garter stitch rows too clearly in that picture, so here’s a close-up of a section:

If you look at the numbers on the bottom edge, 5 is the solid red diamond. Then 6 is next to it, 3 x 2, yellow and blue. Then comes 7, purple. Then 8, which is 2 x 2 x 2, so it’s three sections of blue. Then going out of the picture will be 9 = 3 x 3, so two sections of yellow.

In the center of the shawl, the cool thing is that every diamond represents the sum of the two diamonds that touch its lower edges. See the red and yellow diamond? That would be 5 x 3 = 15. It is the sum of the two diamonds touching its lower edges, which are 10 = 5 x 2 (red and blue) and 5 (red).

Here’s another detailed view, but this time I’ve written in the numbers:

In that picture, see how each number is the sum of the two diamonds below it?

And see how the factorization works? 70, for example, is 7 x 5 x 2, so the colors are purple, red, and blue. 126 = 7 x 3 x 3 x 2, so the colors are purple, two sets of yellow, and blue.

Okay, there are two very cool patterns that I’ve already noticed from looking at the shawl.

First, whenever you’re on a prime row (with a prime on both ends), ALL of the numbers in that row will have the prime as a factor. See how every number in the 3rd row has some yellow? And every number in the 5th row has some red? And every number in the 7th row has some purple?

The reason for that involves the second way you can build Pascal’s Triangle. The rth number in the nth row is the Combination nCr, the number of ways of forming subsets of size r from a set of size n.

Okay, if I’ve just lost everyone, I’ll use examples. The 3rd number in the 5th row can be calculated as 5x4x3/3x2x1 (= 60/6 = 10). The 2nd number in the 7th row is 7×6/2×1 = 42/2 = 21. The 4th number in the 10th row is 10x9x8x7/4x3x2x1 = 10x3x7 = 210. (You always have r factors in the denominator, starting from r and going down 1 each. We call that r! or r factorial. On top, you also have r factors, but they start with n.)

If n is a prime number, all the numbers in that row of Pascal’s Triangle will have n as a factor, and there’s no way it will cancel out with anything in the denominator (except on the very ends when you have 1).

But all that you will notice in the shawl is the color popping up, and you don’t even have to know why. In fact, I planned the shawl by figuring out the sums, and I’d forgotten about the combinations. So I was delighted when I saw that prime factors consistently show up in all prime rows. And then I remembered why.

The second beautiful pattern is related to the sums. The shawl nicely shows the distributive law. If two diamonds next to each other have a factor the same, the diamond above them which they both touch will have the same factor. That’s because ca + cb = c(a + b).

For example, 21 + 35 = 56
and 7×3 + 7×5 = 7(3 + 5) = 7×8

When you combine those two patterns, we’ve got some inverse triangles. Look at the big picture again:

Now focus on the diamonds with red in them. (Red is 5.)

On the row with 5 on the ends, 1 5 10 10 5 1, every number (except the 1s) has red in it. Well, by the distributive law, every number in the next row that touches two of these will have red in it. Those are the three middle numbers on the next row, 15 20 15. The next row will have red wherever it touches two of those, 35 and 35. And finally, we’ll have red in the diamond that touches those two, 70.

The same inverse triangle is going to happen with 7 and purple.

And today I started knitting the 11th row, using pink for 11. So fun! 🙂

Now, I must admit, I’m not particularly pleased with the overall look. The colors looked better in the blanket with rows of white between them. In the shawl, they’re all mashed together and it’s a little bit much with such bright colors. So when I finish this one, I’m planning to make a new one with more subtle differences. I found a wool yarn, Northampton from yarn.com, that has enough slightly different shades of purple. So I’ll be using these colors.

(I still have one more color on order, because the first one I ordered didn’t really go with these.)

The second shawl won’t be quite as good for explaining Pascal’s Triangle, but I think it will be much prettier! I will have to discipline myself to finish the first one before I start it. (I can solve that, I suppose, by using the same needles.)

So there you have it! Pascal’s Triangle knitted into a shawl! I will definitely post again when I finish it!

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Aug 24, 2013February 27, 2016

More about Mathematical Knitting

Mathematical, Prime Factorization 0

On Wednesday, I finished knitting a Prime Factorization Blanket for my new little niece.

In my post about the blanket, I explained how the colors show the prime factorization of each number from 2 to 99. But I didn’t talk about the patterns, and I want to say a little bit about that here.

In fact, the only reason the Prime Factorization Blanket isn’t quite as good as the Prime Factorization Sweater is that I can’t have rows of 8 on the back and rows of 2 and 3 on the sleeves.

And the Prime Factorization Scarf is good for getting the flow of the numbers.

However, I do think the patterns in the 10 by 10 grid are a little easier to see with the larger diamonds on the blanket. Here’s the complete blanket laid out:

Let’s start by looking at the diagonals. 11 is 1 bigger than the base of 10. So the color for 11, red, goes in a diagonal across the blanket from the bottom left to the top right.

9 is 1 less than the base of 10. 9 = 3 x 3, so every number with a factor of 9 has two sections of yellow, the color for 3. You can see the yellows going diagonally up the blanket from the bottom right to the top left.

Oh, and I nearly forgot the more obvious ones. Since 2 and 5 are multiples of 10, they line up in columns. Every second column has turquoise for 2, and every fifth has green for 5.

Once you’re used to focusing on one color, you can pick any color and watch how it distributes evenly around the blanket. Take 19 for example, dark pink. You can see it climb up the blanket from the bottom right to the top left on a steeper diagonal than the one for 9.

And if you look at the colors it’s paired with, first it matches with 2, then with 3, then with two sets of 2, then with 5.

Another fun pattern is that the columns are sets of numbers that are congruent mod 10. So if you add, subtract, multiply or divide any two numbers in the same columns, your result will be in the same column.

For example, 2 + 17 = 19. Well, 62 + 27 = 99. The numbers in the second equation are from the same columns as the numbers in the first equation.

And that’s only the beginning of the patterns you can find.

Now that I’ve mailed off the blanket, I’m consoling myself by getting excited about the Pascal’s Triangle Shawl I’m going to make.

Pascal’s Triangle is formed by starting with 1, then adding a row of numbers where each number below is the sum of the two numbers above it.

Here’s how it works:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1

The cool thing? Even though you’ve got really big numbers, when you factor them, the only prime factors are ones that have already appeared in the triangle. So I only need colors for the prime factors 2, 3, 5, 7, 11, and 13.

I’m stopping at row 15, because on row 16, we’ve got numbers with more than 6 prime factors, and that’s the most I’m prepared to accommodate unless I make my diamonds bigger. But up to 15 is going to be lovely.

I chose colors yesterday and tried to order the same colors. I’m not sure the ones I have aren’t discontinued colors by now, but when my order arrives, I can get going. (In fact, I’ve already started with the colors I have, hoping I won’t have to take out too much.) Here’s the color scheme I chose, using Cotton Classic yarn by Tahki.

2 is on the bottom left, and then it goes around counterclockwise. So 2 will be pale pink, 3 will be rose, 5 will be red, 7 will be purple, 11 will be yellow, and 13 will be turquoise. And they are going to repeat in beautiful ways, just you wait!

I’ve already begun, though if it turns out that the pink I’ve ordered is a different shade from what I have, I’ll have to take out the square for 2 that I’ve begun. But I can’t stand waiting for the order!

You can see there the initial diamond for the first row: 1.

Second row has two diamonds for the second row: 1 1

Third row, I’ve knitted the first diamond for 1, and I’ve begun the next diamond, for 2.

When I get to the row with 4, I will start showing the prime factorization, so 4 will be listed as 2 x 2, with two sections of pink.

The way I’ll show the prime factorization will be exactly like the blanket, but the patterns will be very different, always with the diamond representing the sum of the two numbers on its lower edges.

And it will get cool on the top edge with numbers like 6435 = 3 x 3 x 5 x 11 x 13

I can’t wait to show pictures of the final result. I think it will be beautiful!

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Aug 21, 2013February 26, 2016

The Prime Factorization Blanket!

Mathematical, Prime Factorization 2

Yes! My Masterpiece is finished!

What is this, you ask? This is a Prime Factorization Blanket!

With colors, it shows the prime factorization of all the integers from 1 to 99.

Here is the entire blanket, laid out flat:

Here’s how it works: Every prime number gets a color. The numbers start in the lower left corner.
I left a space for 0.
1 is the background color, white.
Then the next color is 2, a prime, so it gets its own color, blue.
3 is prime, and gets its own color, yellow.
4 is 2 x 2, so that square is two sections of blue. (You can tell on the blanket that there are two sections.)
5 is prime, and gets a new color, green.
6 = 2 x 3, so that square is part blue and part yellow. And so on.

I’ve got 0 through 9 on the first row, 10 through 19 in the next row, then 20 through 29, and so on through the top row, which is 90 through 99.

To show it more clearly, let’s look at each quadrant. Here’s the bottom left quadrant:

I put in the factors for each color. (After a few colors, I stopped putting in the “x” symbol for times.) I put a reference number on the left side so you can easily see which row. This set has 1 through 4, 10 through 14, 20 through 24, 30 through 34, and 40 through 44.

Now let’s look at the bottom right quadrant:

This picture shows 5 through 9, 15 through 19, 25 through 29, 35 through 39, and 45 through 49. For example, see if you can spot 48, which has a prime factorization of 2 x 2 x 2 x 2 x 3. Or look at 38, right below it, which equals 2 x 19.

By the way, this blanket is for my little niece, the daughter of my brother, who is, if it’s possible, even more of a math geek than me. On the 17th of December, my sister-in-law had an ultrasound, and we learned that the baby would be a girl, so I chose shades of pink for the next primes that came up, 17 and 19!

Now here’s the upper left quadrant:

This picture shows 50-54, 60-64, 70-74, 80-84, and 90-94. Can you find 62 = 2 x 31? Or 94 = 2 x 47? (I have to note that the colors are more distinct in person, and you can tell by the garter ridges how many sections there are of each color.)

And finally, the upper right quadrant:

And this, of course, covers 55-59, 65-69, 75-79, 85-89, and 95-99.

I’m so happy to finish it! The yarn is the same as what I used for my Prime Factorization Sweater, Cotton Classic. This yarn has enough colors (most important qualification), and it’s wonderfully soft — perfect for a baby blanket. I used a lot of leftover colors from the sweater, in fact.

The only really hard part? Giving it away! But I got the *idea* because my brother’s wife was having a baby, so this seems only fair to send it to the baby, as promised. Unfortunately, she lives on the other side of the country — so the one stipulation is they must take *lots* of pictures of her with it!

In fact, I thought of a way to console myself for giving away the blanket. My next project will be a Pascal’s Triangle Shawl!

I tested out, and the shape will work great!

I loved doing the entrelac squares for the blanket — it was much much easier than the intarsia I used on the Prime Factorization Sweater. And it will be easy-peasy to make a triangle instead of a square. I’ll use factors and do Pascal’s Triangle…. More on this to come, you can be sure!

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.

Oh, and don’t forget! If you want your own prime factorization t-shirt or tote bag, you can find them at my Cafepress shop.

Apr 12, 2013February 27, 2016

Halfway on the Prime Factorization Blanket!

Mathematical, Prime Factorization 0

I’m halfway finished with my new niece’s Prime Factorization Blanket!

That’s the good news. The bad news is that it doesn’t look like I’m going to finish before Arianna arrives. But the good thing about a blanket is that it doesn’t have a size, right?

I actually finished up to 49 a week ago. I did not take a picture and report my progress. And then — when I started on the next row and began knitting 50 — I discovered I had used the wrong color when I knitted 40! I had used the color for 3 in place of the color for 5! *shudder*

(Those who need to be brought up to speed, I explain the blanket in previous Prime Factorization posts.) 40 should be 2 x 2 x 2 x 5, so the square was divided into four sections, with three of them the color for 2 (blue), and one the color for 5 (green). But, horror of horrors, I had used the color for 3 (yellow)! And I didn’t even discover it until I after I had knitted 50 = 2 x 5 x 5, also using yellow when I should have been using green! Yikes! But then I was getting ready to start on 51 = 3 x 17, and then it dawned on me that the color for 3 is yellow, so it is NOT the color for 5, and I’d been doing it wrong!

Fortunately, it was on the end of the row, and relatively easy to fix. I took out the knitting I’d done on 50, undid the last white square in the row, and then undid just the yellow section I’d put on the top of 40. I replaced it with green, knitted the white square back, and then started up on 50.

But I’ve decided that taking a picture after each row and *checking* the numbers carefully is a good idea!

I did discover a mistake when I finished knitting my prime factorization sweater. I think it was in the rectangle for 48. But 48 has five factors, and in that piece of knitting the factor for three only was about four stitches. So I was able to pick them out and put in the correct color with a crochet hook! It would not be so easy to do on this blanket, so I am going to have to be more vigilant!

My posts on Mathematical Knitting and related topics are now gathered at Sonderknitting.